Каталог статей
Категории статей:
| Общие сведения [9] | Техника складывания [6] | Другие [2] |
Масштабирование в оригами
Для складывания моделей по CP необходимо освоить масштабирование и построение подобных треугольников по трем соответствующим элементам.
Задача. Дан паттерн, вписанный в квадрат со стороной a. Для того, чтобы перенести паттерн на другой лист большего размера (со стороной b) применяют масштабное увеличение.
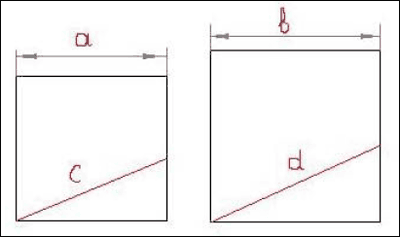
Дано:
Квадрат 1:
- Сторона квадрата равна a;
- Линия, которую нужно перенести – с.
Квадрат 2:
- Сторона квадрата – b.
Необходимо определить длину линейно преобразованной стороны, находящейся в увеличенном масштабе – d.
Решение:
а) Определим коэффициент масштаба – К
Он показывает, во сколько раз будет увеличен линейный размер каждой линии
б) Определим линейный размер искомого отрезка – d.
Подобным образом определяются длины всех составляющих линий схемы в новом масштабе, т.е. коэффициент масштаба умножается на длину известной линии.
Построение подобных треугольников по 3-м элементам
После того как мы определили длины всех сторон, необходимо соединить их так, чтобы все углы между соответствующими линиями были равны, это делается с помощью циркуля и линейки.
Существует 2 метода: последовательный и базовый
Последовательный метод.
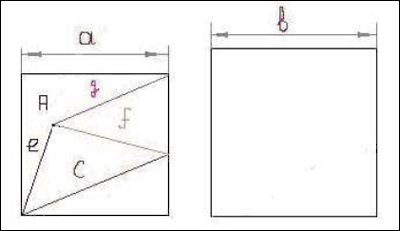
Дано:
Квадрат 1: a, e, c, f, g (смотри рисунок);
Квадрат 2: b.
Необходимо построить все линии в новом масштабе.
Построение:
1) Определим длины всех сторон в новом масштабе (смотри первую задачу); получаем e', c', f', g'.
2) построим первую линию, относительно которой будем строить остальные, для этого проведем циркулем окружность с центром в нижнем левом углу и радиусом равным – c’. Соединяя этот центр с точкой пересечения боковой грани, получим искомую линию c’.
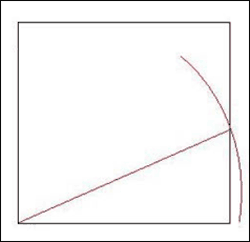
3) найдем место положения точки А, она будет в точке пересечения двух окружностей:
первая окружность: центр – нижний левый угол квадрата, радиус – е’;
вторая окружность: центр – точка пересечения красной линии и боковой грани квадрата, радиус – f’.
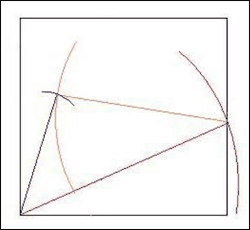
4) Построим точку А’ с правым верхним углом квадрата и получим последнюю недостающую линию.
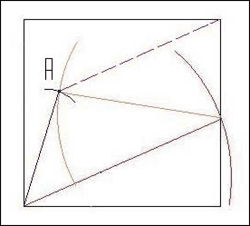
Так последовательно, относительно одной из линий строятся все остальные. Все построения следует делать относительно какой-нибудь фиктивной линии, т.е. определяется какая-нибудь наугад взятая линия, и через ее концы проводятся окружности, при попарном пересечении которых получаются основные точки, через которые будут проходить основные линии схемы. На рисунке за фиктивную линию принята красная, параллельная основанию квадрата.
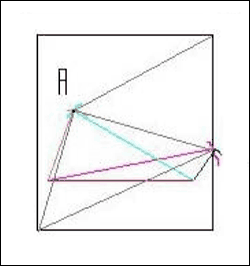
Базовый метод масштабирования
Этот метод масштабирования применяется чаще всего. В нем за основу берется декартова система координат, а основные узлы и точки переносятся на больший лист после определения местоположения точек, относительно осей.
Пример

Чтобы построить эти линии необходимо вычислить следующие расстояния:
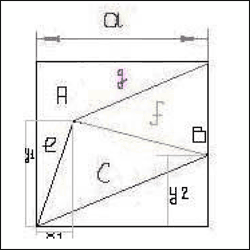
1) Параметры точки А (x1; y1) – снимается с исходного паттерна, и при умножении на коэффициент масштаба получаем приведенные координаты точки А’ (x1’; y1’).
Параметры точки B (a; y2), после умножения на коэффициент масштаба получаем приведенные координаты точки B’ (b; y2’)
2) Строим на чистом листе основные точки схемы, т.е. А’, B’ и достраиваем все необходимые линии.
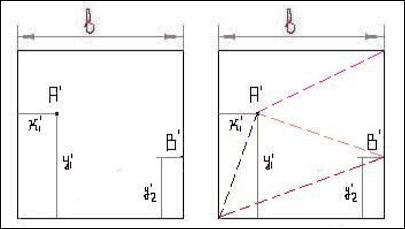
Вот таким образом, рассчитывая координаты всех узлов схемы можно с помощью циркуля и линейки увеличить масштаб.
Комментарии
| Всего комментариев: 10 | |
|
1. iXander
 Спам
Спам
20 Фев 2007, 13:53
А еще у подобных многоугольников (треугольников в том числе) соответствующие углы равны. И, приняв границы листа за координатные оси, можно перенести на новый лист угол между прямой С и нижней границей.И так со всеми основными прямыми. Тогда не нужно вычислять линейные размеры новых элементов - они получаются построением. Но, может быть, это не всегда удобно? 25 Апр 2007, 15:58
Присоединяюсь к iXander-у. Ведь не зря же учили (некоторых) в школе строить равные углы при помощи линейки и циркуля. Для того, кто умеет - это удобно. |
|
Использование материалов сайта разрешается только с указанием прямой ссылки на источник
Сайт управляется системой uCoz