В этой теме рассматриваются и обсуждаются все вопросы по оригами, связанные с математикой. Обсуждаются теоремы оригами и их практическое использование.
Делай, что должен и будь, что будет!!!!))
   | |
| Модератор форума: anermak, univer |
| Форум Oriart Оригами Школа Crease Pattern Математика оригами |
| Математика оригами |
Делай, что должен и будь, что будет!!!!)) |
Вот еще задачка на знание геометрии окр.
Есть поля трех створок, окр - R1,R2,R3... Определить максимальную длину откидной створки окр - r, которую можно получить во внутренней области? 
Делай, что должен и будь, что будет!!!!)) |
Господа математики, для равностороннего треугольника ведь будет такое же решение, как для шестиугольника? Уж больно полезная задача для нас. А то кругом всякие tesselation'ы
Галерея на фликре |
Бывалый
 Сообщений: 90
Откуда: Вольнянск
Нет. Решение немного другое.
 Добавлено (08.02.2010, 15:08:27) Добавлено (08.02.2010, 15:50:47) Quote (anermak) только ты описался Не описался, а очепятался. А то как то не красиво звучит... Добавлено (08.02.2010, 16:08:03)
Post edited by Morkva - Пн, 08 Фев 2010, 15:48
|
Quote (Morkva) Добавлено (08.02.2010, 15:08:27) --------------------------------------------- И где здесь что ? Делай, что должен и будь, что будет!!!!)) |
Quote (Morkva) Задача. Дано две точки N,P и две прямые AB,CD. Построить уравнение складки отражающей точки N,P на прямые AB,CD. построить циркулем и линейкой или все-таки найти ур-ие складки? не очень понятно...
Делай, что должен и будь, что будет!!!!)) |
Quote (Morkva) Найти уравнение. тогда все элементарно )) с учетом того, что у равнобедренной трапеции углы при основании равны... пусть народ развлекается... Еще одна простенькая задачка, но крайне полезная для оптимизации. Построить цепочку Штейнера длины 4, 5, 6, с произвольным выбором центра инверсии... Допускается измеритель ))) Делай, что должен и будь, что будет!!!!)) |
Кому интересно мои небольшие разработки в оптимизации сложных полей, привнесенные в оригами из геометрии окружностей
там же можно найти решение, на предложенную мной задачу        
Делай, что должен и будь, что будет!!!!)) |
Начинающий
 Сообщений: 5
Откуда: Москва, Ростов
Вот у меня вопрос. Кто-нибудь разбирается в математических основах техники непрямых складок? Я имею в виду дифференциальную геометрию, по большей части. Ну, например, вдоль каких кривых можно делать складку? И если можно, то какова степень свободы этой складки? Интуитивно ясно, что там есть одна степень свободы, по крайней мере это так для прямой и окружности.
Меня, как математика, это интересует в теоретическом плане, может заинтересует как оригамиста) Киньте ссылки на статьи, если есть. Лучше ничего не делать, чем делать ничего. |
Quote (zayzi) Я имею в виду дифференциальную геометрию, по большей части Поспрашивайте на форуме прошлогодний номер журнала Jaos special edition, с лошадью камийа, и новую Лэнговскую книжку... там есть...
Делай, что должен и будь, что будет!!!!)) |
Опытный
 Сообщений: 126
Откуда: Омск
Как получить деление стороны листа , как на рисунке приведенном ниже?
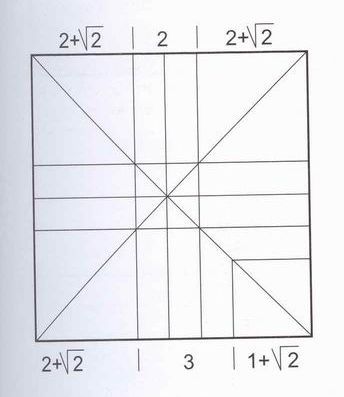 Заранее спасибо.
Прикрепленный файл:
0260203.jpg
(16.0 Kb)
Post edited by Богатырь - Пн, 07 Июн 2010, 02:26
|
| |||