|
Математические досуги
|
|
 A
A
часто-захожу-анонимно
Тема для любителей математики.
Задачи, теоремы, интересные решения.
Не только в связи с квадратом и бумагой - всякие 
Условия задач выделяйте шрифтом и цветом.
|
 A
A
часто-захожу-анонимно
Тема для любителей математики.
Задачи, теоремы, интересные решения.
Не только в связи с квадратом и бумагой - всякие 
Условия задач выделяйте шрифтом и цветом.
|
 A
A
часто-захожу-анонимно
Задача на шахматной доске.
Шахматная доска (тоже, кстати, квадрат  ) породила множество интереснейших задач. Известны задачи на разрезание, расстановку шахматных фигур (ладьи, слоны, ферзи...) ) породила множество интереснейших задач. Известны задачи на разрезание, расстановку шахматных фигур (ладьи, слоны, ферзи...)
Предлагаю старинную задачу:
Задача №1
Обойти стандартную шахматную доску ходом коня, посетив каждое поле только один раз. Это возможно (решиний - много)
Найдите такое решение, при котором, завершив обход доски конь окажется на расстоянии "хода коня" от начальной клетки. То есть, с последний клетки маршрута можно попасть на первую ходом коня.

Решение можно давать и картинкой (соединить центры клеток в порядке прохождения), и последовательной записью ходов (кто знает буквы-цифры) или проставив в клетках номера ходов.
Поскольку решения могут отличаться, не будем ограничиваться одним ответом.
|
 M
M
Crease Master
Сообщений: 1484
Расширяю задачу  (для тех, кто любит посложнее) (для тех, кто любит посложнее)
Задача №2
Для каких значений(N,M,L) фигура - кенгуру(может ходить N клеток прямо и M в сторону на досках L-L, где L>M>N)) может обойти всю доску и вернуться в клетку соседнюю с исходной, побывав в каждой клетке ровно: 1) по одному разу. 2) по К раз...
Делай, что должен и будь, что будет!!!!))
|
Вопрошающий
Сообщений: 39
Quote (zvira) Так приведите хотя бы одно для разгона. Мы же знаем, что их много, поэтому другие любители загадок поищут другие решения
С удовольствием  . Решений действительно очень много... Для начала немного справки о самой задаче: . Решений действительно очень много... Для начала немного справки о самой задаче:
Code Особая популярность задачи объясняется тем, что в XVIII и XIX веках ею занимались многие крупные математики, в том числе великий Леонард Эйлер, посвятивший ей большой мемуар "Решение одного любопытного вопроса, который, кажется, не подчиняется никакому исследованию". Хотя задача была известна и до Эйлера, лишь он впервые обратил внимание на ее математическую сущность, и поэтому задачу часто связывают с его именем.
Значительно труднее проблема, состоящая не в отыскании определенного маршрута коня по доске, а в нахождении всех маршрутов и подсчете их числа. Увы, эта задача не решена до сих пор, и шансов на успех немного. Известно, правда, что число решений не превосходит C63168 (число сочетаний из 168 элементов по 63, оно состоит из ста цифр), но больше 30 миллионов.
Математик Ф. Миндинг, подошедший к проблеме с алгебраической точки зрения, предложил метод, позволяющий вывести формулу для числа всех решений, однако вычисления, которые следует при этом провести, практически неосуществимы.
Литература, посвященная задаче о ходе коня, весьма обширна. Известно много методов для нахождения маршрутов коня, которые носят имя первооткрывателей — метод Эйлера и Вандермонда, рамочный метод Мунка и Коллини, метод деления на четверти Полиньяка и Роже и др.
Если говорить о графиках маршрутов коня, то здесь придумано множество необычных решений, изображающих различные предметы, буквы или знаки (известен даже график, посвященный Наполеону) с получившейся буквой N на доске. Два достопримечательных примера такого рода приведены на этом рисунке.
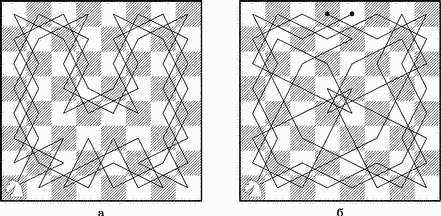
График одного маршрута (он является замкнутым) напоминает собой вазу, а график другого подобен цветку, части которого расположены в высшей степени симметрично.
Цитаты и картинки приведениы из книги Е. Гика: “Шахматы и математика” (в сети http://golovolomka.hobby.ru/books/gik/02.shtml )
В последнем известном мне переиздании этой книги (Аванта+, 2009, E.Гик, "Математика на шахматной доске") начиная со стр. 50 разбираются различные варианты прохождения конем различных досок (квадратных, прямоугольных, фигурных...)
Интересно будет попробовать применить эти выкладки для "кенгуру"Quote (anermak) Для каких значений(N,M,L) фигура - кенгуру(может ходить N клеток прямо и M в сторону на досках L-L, где L>M>N)) может обойти всю доску и вернуться в клетку соседнюю с исходной, побывав в каждой клетке ровно: 1) по одному разу. 2) по К раз...
Спасибо за задачку!
--- описание алгоритмов пришлось удалить, т.к. своих решений ещё не было, а пользоваться готовыми рецептами думающим людям неинтересно.
Подробное описание алгоритмов и вариантов решения будет уместно, когда задачку объявим решённой (хотя бы три человека решат).
Прикрепленный файл:
8032873.gif
(19.4 Kb)
Post edited by zvira - Пн, 06 Июн 2011, 17:55
|
 M
M
Crease Master
Сообщений: 1484
|
 A
A
часто-захожу-анонимно
Для кенгуру (3,1) доска 8*8 обскакивается за 8 мин. (первая попытка):

возможны варианты 
|
 M
M
Crease Master
Сообщений: 1484
Конечно ОДЗ, так ведь ограничивать можно и дальше  Интересно? До какой степени? Интересно? До какой степени? 
Quote (zvira) чётная сумма M+N заставит кенгуру прыгать только по полям одного цвета  если сумма нечетная, то пройти можно редко, это не достаточный признак (конт-пример N=0 М=3, сумма нечетная, а пройти нельзя) Ну, или доска 8-8, N=2, M=3 (старт а1) - тоже нельзя, если понять почему, то задача практически решена. если сумма нечетная, то пройти можно редко, это не достаточный признак (конт-пример N=0 М=3, сумма нечетная, а пройти нельзя) Ну, или доска 8-8, N=2, M=3 (старт а1) - тоже нельзя, если понять почему, то задача практически решена.
а вот ограничивая дальше ОДЗ получается очень интересненько 
___________________________________________________
Решение +1  молодец! молодец!
Делай, что должен и будь, что будет!!!!))
|
 M
M
Crease Master
Сообщений: 1484
Кенгуру(1,0) легко проходит доску, при чем на четных, может даже возвратиться в исходную точку 
Делай, что должен и будь, что будет!!!!))
|
 A
A
часто-захожу-анонимно
Меня волнует другой вопрос: почему школьники на каникулах не хотят совершенствовать свой мозг? Оправданием может служить только оторванность от сети (поход в пустыню, тундру, горы, кругосветное плавание на надувном матрасе...).
Но ведь регулярно включают ПК, задают вопросы ("дайте схему", "хочу книжку"...), а на простой вопрос про лошадку на квадратном поле ответить не могут  Неужели так поглупели после 31 мая? Задачка-то детская. Я имею в виду стартовую задачу темы. Неужели так поглупели после 31 мая? Задачка-то детская. Я имею в виду стартовую задачу темы.
|
 M
M
Crease Master
Сообщений: 1484
Пока кенгуру покоряет новые доски - небольшая задачка на смекалку ))
Задача №4.
На доске написаны квадраты последовательных целых чисел: 1^2, 2^2, 3^2, ... , 100^2, 101^2
Перед каждым из них можно поставить "-" или "+" и затем вычислить алгебраическую сумму.
Какой наименьший неотрицательный результат можно получить? 

Делай, что должен и будь, что будет!!!!))
|
Вопрошающий
Сообщений: 24
Точно не ноль 
Век живи, Век учи́сь!!
|
 M
M
Crease Master
Сообщений: 1484
Таааак !!  Правильно!!(51 нечетный член) Правильно!!(51 нечетный член)  А дальше....,- рассуждаете верно... А дальше....,- рассуждаете верно...
Делай, что должен и будь, что будет!!!!))
|
 M
M
Сообщений: 461
For i = 101 To 1 Step -1
If n - i * i < 0 Then n = n + i * i Else n = n - i * i
Next
результат = 1
Мой flickr
|
 M
M
Crease Master
Сообщений: 1484
|




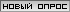


 доска 8-8
доска 8-8 

 Неужели так поглупели после 31 мая? Задачка-то детская. Я имею в виду стартовую задачу темы.
Неужели так поглупели после 31 мая? Задачка-то детская. Я имею в виду стартовую задачу темы.
 ) Это вообще математическая задача
) Это вообще математическая задача